What should you do when you can’t remember the formula or you don’t have enough time to complete the algebraic calculations? Approximating your answer, back solving, and picking numbers are all methods that can be used to determine the correct answer.

 

For example, if the question asks you what is 47% of 200,000? You know that 50% or half of 200,000 is 100,000. So based on the list of answers you would pick the answer closest to but not equal to 100,000 (94,000).

 

Back solving involves working backward from the answer choices. Remember the correct answer is just mixed in with the wrong answers. Select one of the numerical answers and plug it into the problem. If it works then you have found the correct answer. If it does not work then you should be able to figure out whether to select a larger or smaller number.

Here is an example from the ASVAB Kaplan 2015 book that illustrates how to back solve.

 

 

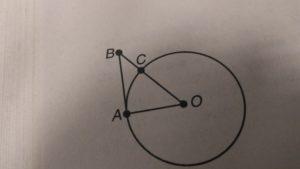
You are given the following information: AO = 6 (circle radius), AB = 10, <OAB is a right angle. What is the length of BC?

Answer choices

(A)   2(√17 – 3)

(B)   4

(C)   2(√34 – 3)

(D)   6

To back solve pick one of the answers. Let’s start with answer (B). If BC = 4 then the hypotenuse (BO) would equal 4 + 6 = 10. The hypotenuse (BO) is always the longest side of a right triangle so this is not the correct answer. Let’s select answer (D). If BC = 6 then the hypotenuse would be 6 + 6 = 12. Now use the Pythagorean Theorem to verify your answer. We have 6² + 10² = 12². We can see that this is not the correct answer because 136 ≠ 144. Now you are left with answer (A) and answer (C). The √136 = 2√34 so the correct answer is (C).

 

When you encounter variables in the problem and the answer choices, you can pick numbers for those variables. Look at the following example from the ASVAB Kaplan 2015 book.

 

For all r, s, t, and u, what does r(t + u) – s(t + u) equal?

 

Answer choices

(A)  (r + s)(t + u)

(B)  (r – s)(t – u)

(C)  (r + s)(t – u)

(D)  (r – s)(t – u)

 

Now replace these variables with some very simple numbers. Let r = 5, s = 4, t = 3, u = 2. You may choose any set of numbers. The original equation becomes 5(3 + 2) – 4(3 + 2) =  25 – 20 = 5.

 

Next substitute your numbers into to each answer to find the correct answer.

 

If more than one choice gave the correct answer, you would need to select another set of numbers and try only the answer choices that worked with the previous set of numbers.

 

Remember you get points for correct answers not for how you got those answers.